Calculating Polygon Centroids: Principles and Implementation

In a previous article "Adding Centroid Coordinates in QGIS Using Field Calculator", we demonstrated adding centroid coordinates via QGIS. This article explains the mathematical principles behind centroid calculation for polygons.

Conceptual Derivation

Consider a square with area = 16:

With uniform mass distribution, its centroid is at (2, 2).

Adding a rectangle (area = 32) with centroid at (6, 4):

The combined centroid (x, y) satisfies:
math
x \times 48 = 2 \times 16 + 6 \times 32 \
y \times 48 = 2 \times 16 + 4 \times 32

Result: (14/3, 10/3)

Extending this to arbitrary polygons by decomposing into triangles yields: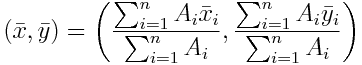

Where:

A_i: Triangle area (calculated via cross product of edge vectors)
(x_i, y_i): Vertex coordinates

JavaScript Implementation

function getCentroid(points) {
    let totalArea = 0;
    let totalX = 0;
    let totalY = 0;

    for (let i = 0; i < points.length - 1; i++) {
        const a = points[i + 1];
        const b = points[i];
        
        // Calculate triangle area using cross product
        const area = 0.5  (a[0]  b[1] - b[0] * a[1]); 
        
        // Calculate sub-centroid (triangle centroid)
        const x = (a[0] + b[0]) / 3; 
        const y = (a[1] + b[1]) / 3; 

        totalArea += area;
        totalX += area * x;
        totalY += area * y;
    }

    return [totalX / totalArea, totalY / totalArea];
}

Validation

Using methods from "Exporting SHP Feature Coordinates to TXT in QGIS", we compared results:

Manual Calculation:

QGIS Field Calculator Output: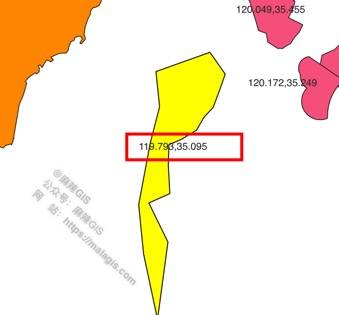

Results match, confirming algorithm accuracy.

MalaGIS
Sharing GIS Technologies, Resources and News.